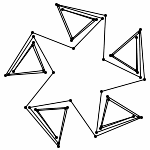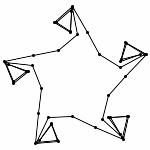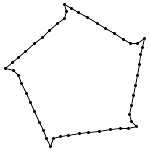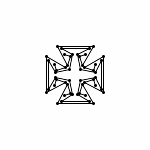
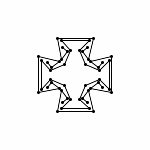
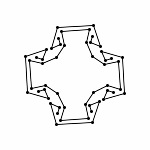
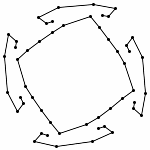
Erik Demaine's Linkage Page: Animations

This page contains still images, and links to animated GIFs, of a motion that straightens and convexifies a few sample linkages. They were generated using the CPLEX solver for linear and quadratic programs, and by using the simple forward Euler method to approximate a solution to the ODE.

Each animations is shown in two forms: with and without zooming. The "natural" view is without any zooming, or more precisely, with a constant viewpoint throughout the motion. This view shows that the motion preserves the lengths of the edges. Unfortunately, because the linkages "expand" a lot, this view makes it hard to see the linkage in the beginning. Thus, the other view, "with zooming," automatically zooms each frame of the animation; in other words, it zooms out during the motion so that visibility is maximized. Of course this has the effect that the edge lengths differ from image to image in this view; but in reality, the edge lengths do stay the same.

If you have a favorite linkage you would like to open, and you can draw it in xfig (one object per connected component), please send it to me and I will animate it as time permits. (It takes a lot of computer time.)

Index of Examples

Currently available are

Tacks and Staples
This example was designed by Joseph Mitchell on July 5, 1999, with some simplifications suggested by Joseph O'Rourke. This is one of the last examples I've seen. It was first unlocked by Joseph O'Rourke on July 8, 1999, using a symmetric motion.

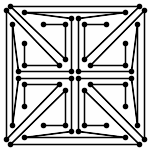
Animation (without Zooming)
Animated GIF (97k)
Antialiased Animated GIF (312k)

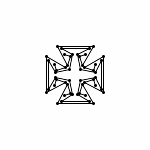
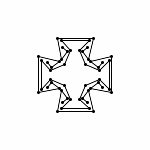
Animation with Automatic Zooming (the edge lengths in fact stay the same)
Animated GIF (121k)
Antialiased Animated GIF (508k)

Teeth
This example is one of the first I saw, designed by Jorge Urrutia. It was never really thought to be locked, but it was noted as difficult to open. The linear program found a rather surprising solution--I was expecting it to pull the two jaws apart.

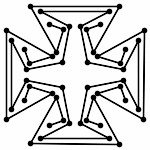
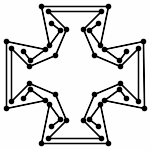
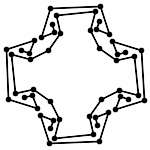
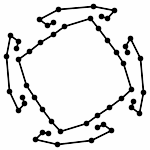
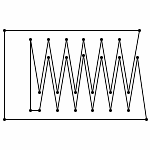
Animation (without Zooming)
Animated GIF (69k)
Antialiased Animated GIF (347k)

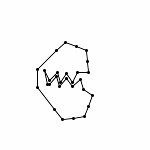
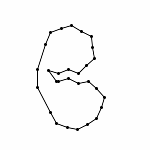
Animation with Automatic Zooming (the edge lengths in fact stay the same)
Animated GIF (252k)
Antialiased Animated GIF (827k)

Doubled Tree
This polygon comes from doubling every edge of an underlying tree. A few people had conjectured that this polygon could not be convexified, because the underlying tree is locked. However, while the tree is locked, the polygon can be convexified; the key difference is that the center vertex is split into several vertices.

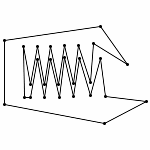
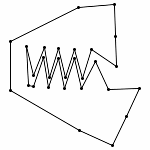
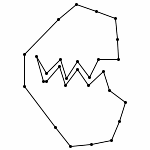
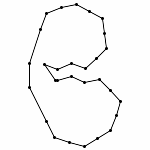
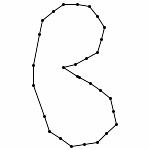
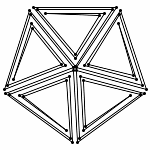
Animation without Zooming
Animated GIF (103k)
Antialiased Animated GIF (418k)

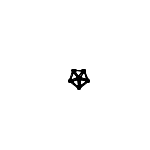
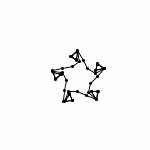
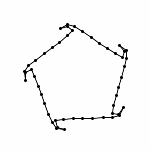
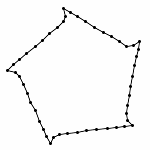
Animation with Automatic Zooming (the edge lengths in fact stay the same)
Animated GIF (274k)
Antialiased Animated GIF (961k)

Acknowledgments

Thanks to Joseph Mitchell for permission to use his examples on this web page, and to William Cunningham for help on solving the linear and quadratic programs.

Last updated July 19, 2007 by Erik Demaine. — Accessibility