Metamorphosis of the Cube

The Metamorphosis of the Cube is a video envisioned and created by Erik Demaine, Martin Demaine, Anna Lubiw, Joseph O'Rourke, and Irena Pashchenko. It appears in a refereed video collection, the 8th Annual Video Review of Computational Geometry, associated with the 15th Annual ACM Symposium on Computational Geometry (SoCG'99). The proceedings contain an accompanying 2-page description of our video.

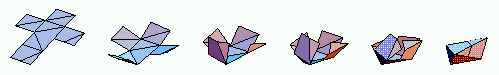
The video is based on our work studying foldings of polygons into convex polyhedra, and the reverse, unfoldings of convex polyhedra into polygons. For more information, see our paper “Enumerating Foldings and Unfolding between Polygons and Polytopes”, the longer technical report “Examples, Counterexamples, and Enumeration Results for Foldings and Unfoldings between Polygons and Polytopes”, and Anna and Joe's original technical report, “When can a polygon fold to a polytope?”.

There are two parts to the video: an animation, and some still frames at the end that briefly describe the video.

Animation

The main part of the video is the animation, which is 2.5 minutes long (4,502 frames at 30 frames per second). The animation is available in three forms, from three different stages of evolution:

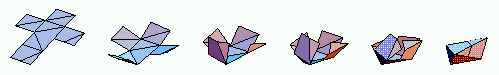
High-quality XviD AVI
POV-Ray with transparency
(25 MB) 		Half-resolution MPEG-1
POV-Ray without transparency
(8 MB) 		Half-resolution MPEG-1
Original in Mathematica
(6 MB)
The latest, modern rendering, in 640x480. You may need to download the free XviD codec, e.g., Windows binaries. The version that appeared in the Video Review, in 320x240 with significant compression artifacts. Should play anywhere. The version submitted to the Video Review, in 320x240 with significant compression artifacts. Should play anywhere.

Unfortunately, the music is unavailable in this electronic version, because we obtained permission from the copyright holder of the song (Philip Glass's Opening) only for the Video Review.

Out of pedagogical interest, you may find interesting the transformation from the original Mathematica rendering to the ray-traced renderings by POV-Ray. The addition of shadows, self-shadows, background, etc. has a major effect. The final, recent addition is the semitransparency, with the goal of better revealing the 3D structure of the polyhedra (in addition to being "in style" these days).

Background Image

Watching the animation, you'll probably notice the old page of cyrillic text in the background. There are a couple of reasons for this. First, it gives something onto which the folding objects can cast shadows. Second, it is in some sense the basis for our work. The page is from a Russian book on Convex Polyhedra by the famous Russian geometer A. D. Aleksandrov. In particular, the theorem underneath the folding cube characterizes what “polyhedral metrics” can be folded into convex polyhedra. The entire page is available as a 1-megabyte JPEG.

Description in the Video

If you have trouble reading the following images, please click on each to enlarge it.

[These foldings and unfoldings illustrate two problems. Problem 1. Unfold a convex polyhedron into a simple polygon. This problem is solved by the star unfolding. (Agarwal, Aronov, O'Rourke, and Schevon 1997)] [But it remains open for cuts along the edges of the polyhedron.] [Problem 2. Fold a simple polygon into a convex polyhedron. Conditions given by Aleksandrov yield an algorithm to find all the ways of gluing pairs of polygon edges together to form a convex polyhedron. (Lubiw & O'Rourke 1997)] [Although Aleksandrov's theorem guarantees uniqueness finding the actual convex polyhedron is an open question. Our examples were done by hand.]

Credits in the Video

Last updated November 28, 2010 by Erik Demaine. — Accessibility