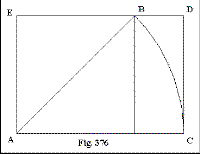
If we have a square, each of the sides of which measures 1 unit in length, the diagonal of that square measures ]/2. In Fig. 376 we see the said square. The diagonal is AB.

The diagonal is laid out along the base- line to AC, permitting us to construct rectangle ACDE. The long side is AC, the short side is AE. This rectangle has thus the proportions of the A-format. But we do not see the sacred cut until we enlarge the diagram by constructing the small square's double-size version.

We see this in Fig. 377 in which the arc CB is extended to point F, after which the double-size version can be entered. We see that line ED is the upper horizontal sacred cut in square FGCA. The A-format is not one particular size. It is a ratio, represented by five basic sizes, each twice (or half) the size of its neighbour.