
The above zebra is an origami model designed by John Montroll. It appears in his book African Animals in Origami, Dover Publications, 1991, pages 94-103.
Another twist on the problem is that the paper may be colored differently on its two sides. For example, wrapping paper typically has a patterned side and a white side, and kami (common origami paper) typically has a colored side and a white side. If you are wrapping a gift, you probably want only the patterened side of the paper showing. If you are folding origami, say out of paper that is black on one side and white on the other, you might want to use the two colors to produce a particular effect of colors showing at different places in the shape. For example, it is possible to fold a single square of paper into a black-and-white checkerboard or a zebra with its stripes.

The above zebra is an origami model designed by John Montroll.
It appears in his book African Animals in Origami, Dover Publications,
1991, pages 94-103.
This result was proved by Martin Demaine, Joseph Mitchell, and myself. We also give three algorithms for optimizing various metrics of the folding. For example, if we can choose the piece of paper to be a thin rectangle, we can wrap a polyhedron with arbitrarily little wastage of paper: the amount of double coverage can be reduced to as close to zero as desired. Alternatively, you can specify the locations of the seams (visible edges or creases of paper) in the wrapping, according to any decomposition of the faces into convex polygons. In particular, unless the faces have holes, there are methods for optimizing the number or total length of seams. (If the faces have holes, some of these problems become NP-complete, while others are conjectured to be NP-complete.)
For more information, you can read our paper ``Folding Flat Silhouettes and Wrapping Polyhedral Packages: New Results in Computational Origami.'' The latest version appears in Computational Geometry: Theory and Applications (2000). The paper also appears in the Proceedings of the 15th Annual ACM Symposium on Computational Geometry (1999), and in the Proceedings of the 3rd CGC Workshop on Computational Geometry (1998).
Joseph O'Rourke briefly describes this work in his ``Computational Geometry Column 36,'' which appears in International Journal of Computational Geometry and Applications, volume 9, number 6, pages 615-618; and SIGACT News, volume 30, number 3, issue 112, September 1999, pages 35-38.
More generally, what is the largest scaling of a given shape that can be wrapped by a given piece of paper? The decision version of this optimization problem is, given a desired shape and a piece of paper, can the shape be wrapped by the piece of paper?
Most of these problems remain open. Several specific instances have been explored, with conjectured optimal solutions, in Serhiy Grabarchuk's Wrapping Puzzles. One version that has been explored more rigorously is wrapping a cube with various rectangles. Another such variation is disk hiding. Both of these topics are described below.
The only instance of wrapping of which I know that has been solved is wrapping a cube with a square. The solution has been conjectured for a while. For example, John Conway showed it to me at a conference in 2000. A picture of the solution is shown on MathPuzzle and on Juergen Koeller's Origami Cube page. That this solution is optimal was finally proved by Michael L. Catalano-Johnson and Daniel Loeb in ``Problem 10716: A cubical gift,'' American Mathematical Monthly, volume 108, number 1, January 2001, pages 81-82 (posed in volume 106, 1999, page 167).
Two interesting variations on the cube-wrapping problem are posed by Henry Larson, in ``Problem 628: A Cube Pattern Puzzle,'' Journal of Recreational Mathematics, volume 10, number 2, 1978, page 129. A rectangular 9-by-12 piece of paper can be cut into either a union of six squares (hexomino) or into an arbitrary connected polygon, and then that cut-out piece must be folded into the largest cube possible. Solutions to these puzzles appear in Journal of Recreational Mathematics, volume 11, number 3, 1978, pages 219-223. The first puzzle was solved by Kenry A. Kierstead, and can be solved by enumeration; the resulting side length of the cube is around 3.053. The second puzzle was solved by Racine Carré with assistance from the poser: there is a way to wrap a cube with surface area arbitrarily close to the area of the rectangle, based on cutting and folding it into a thin strip. This method works for any rectangle.
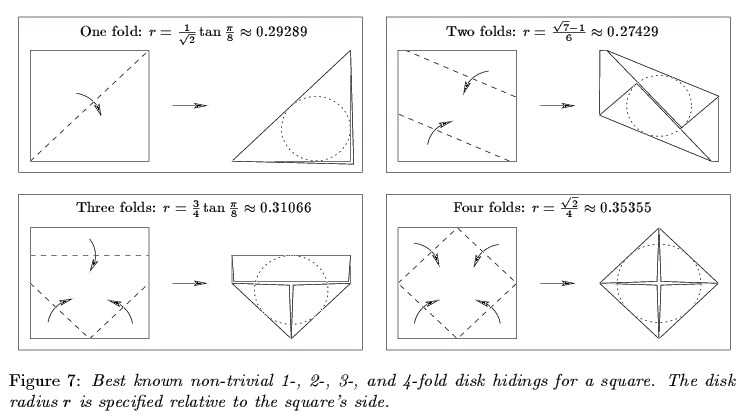
The initial paper on this problem is ``Hiding Disks in Folded Polygons,'' by Therese Biedl, Martin Demaine, Anna Lubiw, Godfried Toussaint, and myself, which appears in the Proceedings of the 10th Canadian Conference on Computational Geometry. We distinguish wrappings by how many simple folds they require. (A simple fold is a fold along a single line.) For folding a square with 2, 3, 4, or more folds, we give conjectured optimal wrappings of the largest disk, which remain open. In the following figure, we give the best known ``nontrivial'' foldings with k folds, nontrivial in the sense that they do not approximate the solution for j folds for j < k. Only the 1-fold case is known to be optimal. The conjecture is that 5 folds do not help.
The most interesting general result is when just a single fold along a line is allowed. What is the largest disk that can be hidden by a single fold of a given polygonal piece of paper? If we unfold the hiding and examine the top and bottom copies of the disk, we discover that any such hiding determines two disjoint equal-radius disks packed in the polygonal piece of paper, and vice versa:
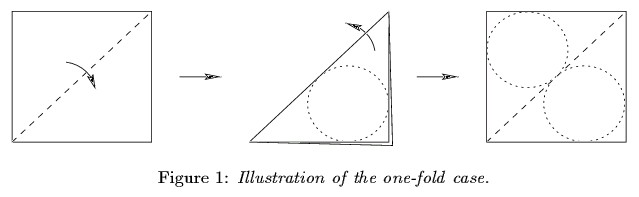
Thus, the problem becomes this: what is the largest pair of nonoverlapping equal-radius disks that can be packed into a given polygon? We proved that this question can be answered in polynomial time. Specifically, for convex polygons, our algorithm runs in O(n2) time on a real RAM, and for nonconvex polygons, it runs in O(n2) time multiplied by the number of bits desired in the answer. (This last part is required for solving degree-8 polynomial (monomial) equations.)
Recently, this problem has been explored in several followup papers. The references are given below. For convex polygons, Bose, Czyzowicz, Kranakis, and Maheshwari (1998) developed a linear-time algorithm, and Kim and Shin (2000) developed an O(n log n)-time algorithm. For simple polygons, Bespamyatnikh (1999) developed an O(n log3 n)-time algorithm using parametric search. For general polygons with holes, Bose, Morin, and Vigneron (2001) have developed a randomized O(n log n)-time algorithm.