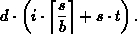
High Performance Computing Symposium 1996
Evaluating the Performance of Parallel Programs in a Pseudo-Parallel MPI
Environment
By
Erik Demaine
Graduate Student
Department of Computer Science
University of Waterloo
03-Feb-1996
Waterloo, Ontario
Canada N2L 3G1
Phone: (519)725-5939, Fax: (519)885-1208,
e-mail: edemaine@mit.edu
LIST OF FIGURES TABLES &CHARTS
ACKNOWLEDGEMENTS
This work was partially supported by Natural Sciences and Engineering Research
Council of Canada (NSERC).
VITA
Erik Demaine
28-Feb-1981
Born in Halifax, Nova Scotia (Canada)
Obtained BSc at Dalhousie University.
Currently a Research Assistant at the Department of Oceanography of
Dalhousie University, and a Graduate Student in Computer Science at the
University of Waterloo.
Research interests include parallel computing, parallel algorithms,
finite-element computations, and computational geometry.
Publications
Demaine, Erik D., and Sampalli Srinivas. 1995. ``Direction-First e-cube: A New
Routing Algorithm for k-ary n-cube Networks.''
In High Performance Computing Symposium '95.
Demaine, Erik D. 1994. ``Heterogeneous Organization for Parallel Programs
(HOPP): A Novel Message-Passing System on UNIX-based Networks.''
Honours thesis, Department of Mathematics, Statistics and Computing Science,
Dalhousie University.
Demaine, Erik D. and Sampalli Srinivas. 1994. ``A Classification Scheme for
Routing
Algorithms on Direct Networks.'' APICS Annual Computer Science Conference
Proceedings, pp. 30-31.
ABSTRACT OF PAPER
Evaluating the Performance of Parallel Programs in a
Pseudo-Parallel MPI Environment
By Erik Demaine
This paper presents a system for use with the message-passing
standard called MPI (Message Passing Interface) that provides a means of
automatically simulating a distributed-memory parallel program. This allows one
to evaluate a parallel algorithm without the use of a parallel computer.
The system consists of three parts: the network evaluator, logging library, and simulator. The network evaluator is a parallel program that evaluates the network speed of a distributed-memory parallel computer. The logging library, when used, automatically logs the message-passing activity of the running program. The logs are designed so that running the ``processors'' on a uniprocessor workstation does not affect the contents. The simulator is a serial program that reads a log generated by the logging library and timing results from the network evaluator, and simulates the execution of the parallel program. In doing so, it emulates an arbitrary direct network architecture. The output includes estimated parallel execution time and speedup.
In this paper, we present how these parts were developed and test them using two merge-sorting algorithms and two Cholesky factorization algorithms. We evaluate these algorithms on a truly parallel network of IBM RS/6000s, and under the proposed system. Results show that the simulation is very accurate.
MPI (Message Passing Interface) [6] is a message-passing standard defined by the MPI Forum. The forum consists of universities, research centers, national laboratories, and multi-national high-performance-computing vendors. MPI was designed by over forty organizations and sixty people. The initial version, MPI1 [2], was published in June, 1993. The latest MPI (1.1) [8] was published in late 1994. The goal is to create a universal communication language implemented on all parallel systems. The MPI Forum studied the existing message-passing systems; instead of taking one as the ``standard,'' they took the most attractive features out of these systems. MPI is based on CHIMP, PICL, EUI (for IBM SPx), Zipcode, p4, CMMD (for CM5), TCGMSG, PVM, NX (for Intel NX/2), PARMACS, Express, and Chameleon [8]. The main advantage of MPI is portability; it has been implemented (both in public domain and commercially) on a variety of parallel systems and networks of workstations.
MPI allows portable libraries to be developed for use with user programs via the profiling interface. This enforces that all MPI implementations provide a separate version of the library with each routine MPI_Xxxx renamed to PMPI_Xxxx, allowing one to write another library with names of the form MPI_Xxxx which do some extra processing before and after a call to the corresponding PMPI_Xxxx. This allows a user to link in a separate set of libraries to facilitate, for example, a logging mechanism that records program activity, without changing their code at all.
Many free MPI implementations support pseudo-parallelism, that is, processor-parallelism may be emulated on a single workstation. This is particularly useful when a researcher wishes to test out a parallel algorithm that s/he has just developed. S/he need not waste valuable supercomputing resources in this case where they are not needed (the algorithm may not work). Once the program is tested, it can be run on a parallel computer for performance benefits. Another useful feature of pseudo-parallel systems is for educational purposes: supercomputing resources are not required to learn parallel programming.
Several MPI profiling libraries have been developed [1]. Unfortunately, all of them rely heavily on a shared real-time clock and record events of a program execution with this value. When the MPI program is run in a pseudo-parallel manner, this does not provide data useful for predicting behavior in a truly parallel environment. First, since multiple processes must share the machine, each pseudo-processor effectively sees the machine at 1/n th of its speed, where n is the number of pseudo-processors (we do not take into account the operating-system overhead of context switches, making real-time values even worse). Thus, if the program is completely parallel, no speedup would be reported by a typical MPI profiling library. Second, communication is measured incorrectly: on a single uniprocessor workstation, no network is involved and the operating system converts ``message passing'' to shared-memory references, which are often much faster operations. Even on a parallel computer, using real-time often yields incorrect results: the latest supercomputers, as they rarely cost under US$10,000,000 [4], are often shared, and so both the CPU and network speed viewed by the profiling library are inaccurate.
Thus, on both pseudo- and truly-parallel computers, the existing MPI profiling libraries are insufficient when full parallelism is not available. The proposed system attempts to remedy this problem by proposing a set of tools including an MPI profiling library that is based primarily on CPU time and ignores communication time. It is based on the assumption that a program consists of computation and communication, ignoring other factors such as I/O. The simulator (another tool provided) takes the logs along with information about a network, and estimates true parallel execution time and speedup based on this network. Finally, the network evaluator is a program that estimates the network speed assuming that the computer is dedicated to running the evaluator.
The system is useful in several ways. It allows effective evaluation of parallel programs without the use of a parallel computer (that is, on a pseudo-parallel machine). Researchers can implement various parallel algorithms and compare their running times and speedups. When one technique is chosen, it can be run on a supercomputer without any change to the program's code. Students can implement and test parallel programs and can also compare them; no supercomputing resource at their university is required. In fact, a student can estimate program runtime on any distributed-memory supercomputer, testing different topologies and speeds of the network. Assuming sufficient memory is available on the workstation, as many (pseudo) processors as desired may be used, thereby testing scalability of algorithms without a massively parallel computer.
The rest of this paper is outlined as follows. Section 2 presents the logging-library part of the system. In Section 3, we discuss factors in parallel computer simulation, the simulator, and the assumptions that it makes. Section 4 describes the network evaluator and the statistical methods that it uses to gather data. We present results validating the proposed system in Section 5. Finally, we make concluding remarks and list possibilities for future work in Section 6.
The logging library is an MPI profiling layer which can be added to any MPI program at runtime, that automatically logs the point-to-point activities of the program. These logs are written in a portable and easily extendible format. Each line in the file forms an entry; each entry is split into a series of words. The first word specifies the processor number associated with the entry, and the second word gives the MPI routine that generated the entry. The third word gives the CPU time consumed in the block of code previous to the entry. The logs do not measure real-time so that running the program in a pseudo-parallel manner or on a heavily loaded system will not affect the results.
The meaning of the remaining words is summarized as follows. The initialization and finalization routines, MPI_Init, MPI_Finalize, and MPI_Abort, take no extra words. MPI_Send, the standard point-to-point send operation, takes the destination node, message tag (a value that must be matched on receive), and size of the message (measured in bytes). MPI_Recv (the corresponding receive operation) takes the same extra words except that the source node is recorded rather than the destination node.
Since real-time is not recorded in the log files, the communication time must be simulated. We do this after program execution in a serial manner to allow the user to simulate the same program on different machines. The simulator accomplishes the task of scheduling the events, calculating an approximate real-time that each event would have occurred on an unloaded truly parallel system. The network speed and topology are specified to this program and a simulation is carried out to evaluate message arrival times, and therefore calculate an estimated parallel execution time. Currently the simulator assumes that messages can be instantly injected into the network, although they are delayed in traversing the network. Further, it assumes that there is no software overhead in the message-passing calls, such as copying buffers. Thus, a process is be said to be idle when it is waiting for a message to arrive (we assume that send and receive operations are non-blocking and blocking, respectively).
As mentioned above, the parallel execution time is estimated. In addition, the computation blocks are summed to estimate the serial execution time, thereby yielding an estimated speedup. This is by no means accurate; however, it gives the user a rough idea of where the algorithm stands. It is best if an optimal serial algorithm is also implemented on the same system that the parallel program was executed on, and the comparison is done by hand to calculate speedup.
Three other results are generated by the simulator. The first is a rough ASCII timeline showing at what points in time the various processors are utilized, and at what times they block, waiting for a message to arrive. This is useful in that the user can quickly find major points in the program where optimization is needed. Furthermore, this can be done using any system (graphics support is not required), and it may easily be printed. The second result gives the percentage of time that each processor was utilized. This information can be examined to determine if the load distribution scheme is fair, or if some processors need results long before they are computed.
Finally, an Upshot log file is generated. Upshot [7] is an X-Windows program to graphically display arbitrary (real-time) log files. The logs generated by the simulator represent the estimated real-times during which processors were computing and during which they were blocking.
The simulator assumes a direct interconnection network. This can be modeled by a directed graph on the processors, where an edge connects processors p and q if p can send a message to q via a single link. Therefore, one specifies a topology to the simulator via the incidence lists that define the graph. That is, for each processor, all the processors that the processor may send to directly are listed. Because we model the network as a directed graph, the links need not be bi-directional.
To achieve a fast simulation, we do not simulate the actual routing of messages. Instead, we use a model that approximates, given two nodes p and q, how long it takes to send a message from p to q. (Currently the simulator only supports point-to-point events, that is, basic send and receive operations.) As an initialization phase, the optimal routing paths for all nodes are calculated; thus the number of ``hops'' for each pair of nodes is known. With this information, a fairly complicated model is used to approximate latency (note that it does not take into account the busyness of links).
We assume that the message must be split into blocks of size b, and that these blocks must be transmitted together through the network, that is, they all move in a group node by node (this is the packet switched or store-and-forward model). Let t be the time to send a byte between two adjacent nodes once the initialization time i has been spent, let s be the size of the message (in bytes), and let d be the distance between the two nodes. Then under the current model, the total time to transmit the message is
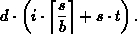
In the following section, we will discuss how to calculate i and t. At the moment, b is not used (it is assumed to be larger than any s).
In the previous section we mentioned the three parameters of the current computation model, t, i, and b. The time to send a single byte when no overhead is taken into account, t, is often specified by network or parallel-computer vendors. However, the other parameters are often difficult to determine. Hence we developed a portable MPI program, the network evaluator, to determine these parameters (assuming that the model holds on the system). It must be run on the parallel system in a dedicated mode (that is, there should be minimal other activity in the system) for accurate results to be obtained. Only two processors are used, that is, only one link's performance is measured; it is assumed that all links have the same performance.
The method used to calculate the model parameters is, on the surface, simple. The program measures the time to send a message (by dividing the round-trip transmission time by two) for various sizes of messages. However, we want this measuring to be extremely robust, so that the final task is to do a linear regression or modification thereof (to incorporate block size). Although it is ``required'' that the system be in a dedicated state, it is impossible to do this. Especially on a LAN-based network, it is difficult to stop occasional network traffic generated by the operating-system, even though we wish to simulate such an environment. Another consideration is the overhead of obtaining the current real-time. We do not want this to interfere with the actual communication; it may greatly affect results for small messages.
To achieve robustness, we must send several messages per message size. One obvious way to achieve some robustness is to time the RTT (round-trip-time) for several messages to be sent, and then take the (arithmetic) mean. This diminishes the overhead in determining the current real-time, but does not abolish the variance of message passing. One reason for this is that the mean is never an actually observed value. We expect that most values are almost exactly the same, but one or two outliers may deviate enough to destroy the mean unless many observations are made.
An alternative is to measure each RTT individually, and take the median of the times. This has two main advantages. First, the median is always an actually observed result. Second, it accurately measures the true message-passing time even when outliers are present.
The disadvantage of the median method is that the real-time clock is checked twice for every message sent. This can cause a significant amount of overhead. To compensate for this, we adopted a mixed median-mean approach which combines the advantages of both techniques. The mean approach is used several times, and then the median of these results is taken. The real-time clock is not examined as often, and outliers which destroy one or two mean values are removed by the median process.
The network evaluator uses the mixed median-mean approach to effectively evaluate the network performance automatically.
To ensure usefulness of the proposed system, several tests were performed. There are two major parts which must be evaluated: the network evaluator and the simulator.
The network evaluator was tested on two bus networks in our lab.
One is the normally used Ethernet LAN that connects all the IBM RS/6000 systems
in the lab. This has an approximate bandwidth of 10 megabits per second.
The other network is a 100 megabits per second FDDI network.
The measurements made by the network evaluator are shown in Figures 1-3.
Figure 1: Raw data for Ethernet.
Figure 2: Data from Figure 1 with outliers removed.
Figure 3: Raw data for FDDI network.
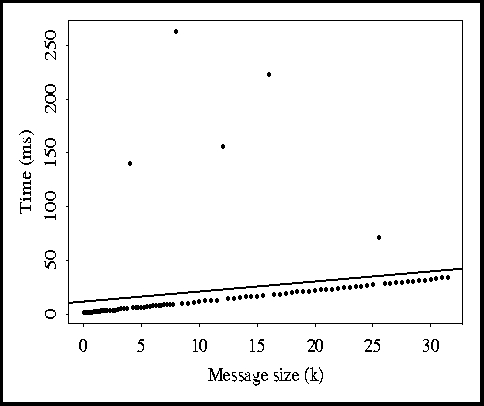
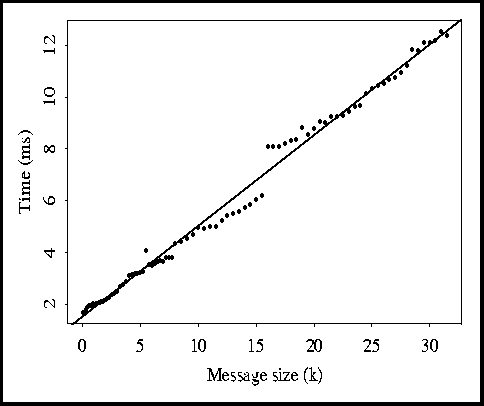
Figure 1 shows the exact data for the Ethernet LAN with little other activity
on the network. Unfortunately, this quite notably has
outliers. These have been removed (currently by hand), yielding the
results in Figure 2. In all figures, a least-squares line fit is shown.
Note that with the outliers removed, the accuracy of the approximation greatly
increases. This can be measured using the residual standard error , which drops from 40.2 ms down to 0.17 ms. This small value (0.17)
indicates that the Ethernet is well approximated using a linear model (once
outliers are removed).
, which drops from 40.2 ms down to 0.17 ms. This small value (0.17)
indicates that the Ethernet is well approximated using a linear model (once
outliers are removed).
On the other hand, the FDDI network has a much more complicated behavior, as illustrated in Figure 3. The linear model poorly approximates the data because of ``jumps'' in the data. Particularly noticeable is the nearly 2 ms jump when 16k is reached. This unexpected behavior makes the current network model unsuitable using the current regression techniques. It is possible that the block size of the model (see Section 3) may be used to compensate partly for the large increase; however, it is not yet known how this can be measured effectively. In the future we hope to solve this problem.
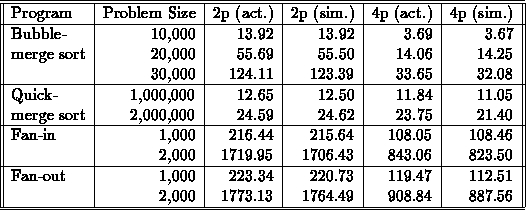
Table 1:
The evaluation of the simulator involved four test programs. The first two implement a parallel merge sort by evenly distributing an integer array among the processors. In the first phase, each processor does a local sorting operation on its data; one program does this using the bubble sort technique, and the other uses quicksort. Second, even-numbered processors merge their data with the odd-numbered ones, leaving the result in the former. To do this, odd processors issue a send to the corresponding even processor, which simultaneously issues a receive. The even processor then merges the two data sets. In the next phase, processors 0 and 2, 4 and 6, and so on, merge their data. After log p phases (where p is the number of processors), the final result lies in processor 0. We use bubble sort since it yields a reasonable speedup (because of the large amount of computation), and we use quicksort to obtain more realistic results.
The last two programs implement the fan-in and fan-out algorithms
[3], respectively,
for reducing a symmetric positive-definite (full) matrix A into the form
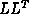 , where L is lower-triangular. This is a major part of
scientific applications wherein linear systems must often be solved.
The basic Cholesky factorization process is split into two phases:
normalization (dividing elements by the diagonal element), and
updating (subtracting a multiple of one column from another).
Fan-in and fan-out both distribute the matrix by columns,
so that normalization is local. We chose to use a ``wrapping'' distribution
wherein processor
, where L is lower-triangular. This is a major part of
scientific applications wherein linear systems must often be solved.
The basic Cholesky factorization process is split into two phases:
normalization (dividing elements by the diagonal element), and
updating (subtracting a multiple of one column from another).
Fan-in and fan-out both distribute the matrix by columns,
so that normalization is local. We chose to use a ``wrapping'' distribution
wherein processor 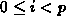 gets columns i, p + i,
2p + i, etc.
There is one identifying feature that differentiates fan-in and fan-out:
fan-in does normalization after updating, whereas fan-out does updating first.
gets columns i, p + i,
2p + i, etc.
There is one identifying feature that differentiates fan-in and fan-out:
fan-in does normalization after updating, whereas fan-out does updating first.
The serial versions of fan-in and fan-out are in fact identical, but the parallel versions differ substantially. The fan-out algorithm, exploiting agenda parallelism, sends each column to all the processors requiring it; whenever a column is received, it is used to update all columns that it affects. On the other hand, the result-based fan-in algorithm loops over columns; if the local processor does not own the column, all the columns that affect it (combined to take space equivalent to a single column) are sent to the owner, and if the local processor owns the column, it collects the information and updates that column.
Because of the inaccuracy of the linear model for the FDDI, this network was not used; instead, we opted to test the programs on the Ethernet. We did this with Argonne National Laboratory's implementation of MPI, called MPICH [1], on four identical IBM RS/6000s. We also ran these programs under the proposed system on one of these workstations, using the model calculated from Figure 2 and a completely connected network. The goal is for these results to be approximately the same.
As Table 1 shows, this goal was reached. The simulated and actual times for the coarse-grain merge-sort algorithms are very close for two and four processors. This also holds for the fine-grain fan algorithms, which involve a tremendous amount of message passing (the log files often reach hundreds of kilobytes).
One may note that the simulation times for the four-processor fan algorithms have a considerably higher error than the other cases. There are two possible explanations for this, both of which are likely affecting results. First, the CPU times measured are so inaccurate that many computation blocks may be measured as taking no time. This would explain why the simulated data (which uses CPU times) is smaller than the actual data for the finest-grain cases. On the other hand, this explanation would imply that the 2,000 case would be measured more accurately than the 1,000 case, since the computation blocks are longer in the former case. The contrary of this may be due to the fact that we are simulating a network with many links, as opposed to the bus that was used for actual times. This would explain why the 2,000 case is less accurate, since more data was sent across the network, causing network contention.
More than four identical IBM RISC/6000 computers were not available.
However, the proposed system has the ability to simulate an unlimited number
of processors and still accurately determine performance. We tested the
sorting programs using up to 16 simulated processors. Speedups are shown in
Figure 4. It should be noted how the simulator calculates speedup.
Figure 4:
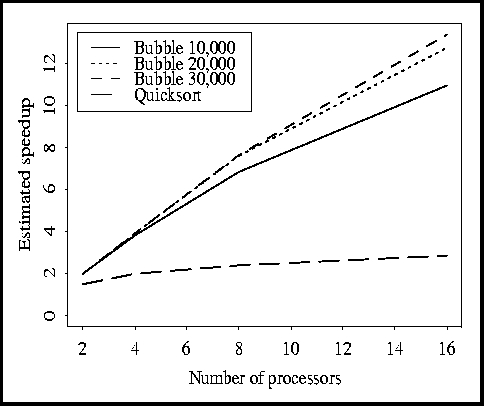
Looking at parallel execution times alone, one deduces that the bubble sort achieves superlinear speedup. This is because doubling the number of processors causes the amount of computation to drop by four times. The simulator, however, compares the amount of computation for several processors (not just one) to the total parallel execution time, thereby yielding sublinear speedups. This gives more insight as to how well the program is performing.
We also tested the 10,000-size bubble-merge sort with the ring topology.
(We chose the bubble-merge sort over the quick-merge sort because of the
high speedup; it would be disastrous to reduce the topology for an already
poor parallel algorithm such as quick-merge sort.)
Note that the communication pattern only requires a hypercube (although it was
simulated with a fully connected network). The results are given in Table 2.
Table 2:
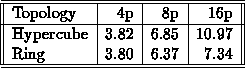
Note that the speedups differ for the hypercube and ring using four processors, even though these topologies are structurally the same. This is because of the numbering of the nodes: in a ring, adjacent nodes can differ by more than one bit, whereas in a hypercube, adjacent nodes differ by exactly one bit.
Although there is no significant benefit for the extra links in the eight-processor hypercube, the hypercube gives substantial improvement over the sixteen-processor ring. As one can see, it is easy to estimate performance for a ring-based (or other topology-based) supercomputer using the proposed simulator. In addition, multiple topologies can be tested and compared - this can be done without rerunning the programs. For example, one could compare a program's performance on a Cray T3D and an Intel iWarp, which have a 3-D torus and hypercube topologies, respectively, without access to these machines (assuming that the models are supported and the network-evaluator data has already been collected).
We have presented a system to simulate the effectiveness of MPI programs using a pseudo-parallel system. To ensure results are accurate, a network evaluator has been proposed to determine true network performance. Finally, we evaluated the system with two merge-sort algorithms and two parallel matrix algorithms, comparing the output with a true parallel system, yielding promising results for the simulator.
One possibility for future work is the improvement of the current communication model (point-to-point). There are two areas in which this extension could be made. First, more switching and network models could be added to support, for example, wormhole routing and bus networks. Second, a more detailed simulation could be done, wherein the routing of packets is considered instead of a simple approximation. This effectively measures bursty traffic and congestion, and allows various routing algorithms to be tested. However, as it is likely a costly process, the option of detailed or approximate simulation should be left to the user.
Another possibility for future work is support for more communication models. These include multicasting, broadcasting, non-blocking, and synchronization communication support. As the system stands, this communication is not measured, and so is ignored.
Although MPI is becoming widely used, another message-passing system called PVM (Parallel Virtual Machine) [9] is even more common. PVM, which is essentially the only competitor of MPI, is based at Oak Ridge National Laboratory. Porting the proposed system so that it supports PVM programs as well would make it more widely accepted.
Finally, as mentioned in Section 3, an Upshot log is generated by the simulator. Further work includes examining the use of Upshot logs for understanding, debugging, and optimizing programs. We also consider creating logs in PICL format, which allows the Paragraph [5] system to be used. This mature program can also be examined for use in program evaluation.
[an error occurred while processing this directive]