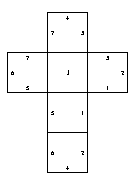
In the video ``Metamorphosis of the Cube'' we show the five polyhedra that can be obtained by edge-to-edge gluings of the Latin cross (where the edge of length 2 is viewed as two edges of length 1). This was originally mentioned in the paper ``When Does a Polygon Fold to a Polytope?'' by Anna Lubiw and Joseph O'Rourke, and the crease patterns are shown on David Eppstein's Geometry Junkyard.
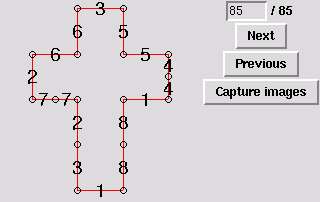
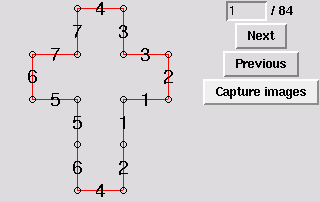
It is even more surprising how much more is possible with non-edge-to-edge gluings. Koichi Hirata wrote an excellent program to compute all the possible gluings of a given polygon into convex polyhedra. The results are shown graphically below. This list was independently verified by a program written by Anna Lubiw. We have tried all of these gluings by hand, and determined the (unique) crease patterns that permit folding into convex polyhedra. These are also shown below.
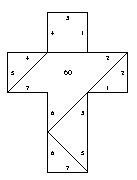
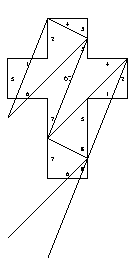
The following gluings and foldings are in no particular order. In each case, the gluing is shown (equal numbers are glued together), and the crease pattern is shown if it is "unique." Crease patterns can be clicked on to obtain printable PostScript.
All gluings except the cube come in symmetric pairs, because the Latin cross has reflectional symmetry. Thus, some gluings are simply marked ``Gluing symmetric to n'' This means that the gluing and the crease pattern can be obtained simply by reflecting those for n. In each case, we also give a brief description of the resulting polytope. When it is the same as a previous polytope, or the mirror reflection of a previous polytope, this is noted. (This characterization is all done by hand, but we have double-checked that it is correct.) The result is 21 distinct polytopes that can be folded from the Latin cross.
1. Cube [edge-to-edge]
2. Octahedron, six degree-4 vertices
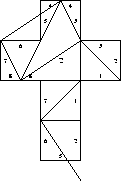
3. Reflectionally symmetric pentahedron, six degree-3 vertices
4. Same polytope as 3
5. Octahedron [edge-to-edge]
6. Mirror polytope of 2
7. Same polytope as 3
8. Same polytope as 3
9. Mirror polytope of 2
10. Same polytope as 2
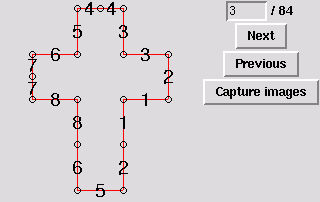
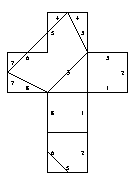
11. Hexahedron, three degree-4 vertices and two degree-3 vertices
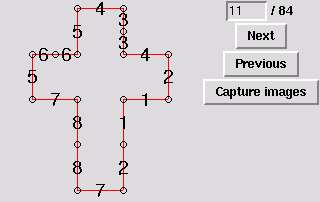
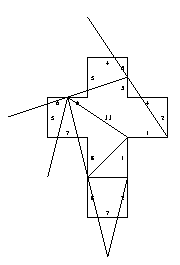
12. Reflectionally symmetric pentahedron [edge-to-edge]
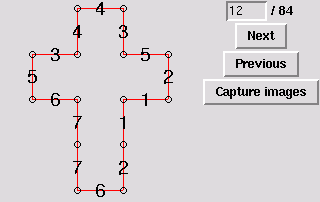
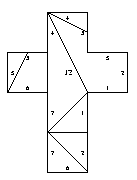
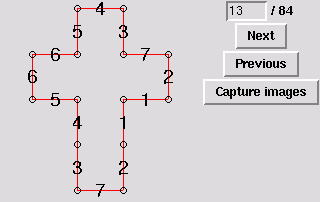
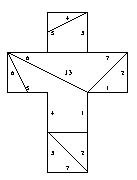
13. Same polytope as 12 [edge-to-edge]
14. Mirror polytope of 11
15. Mirror polytope of 5 [edge-to-edge]
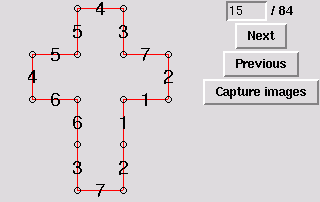
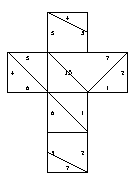
16. Gluing symmetric to 9
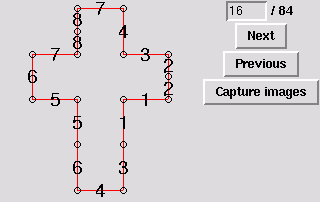
17. Gluing symmetric to 3
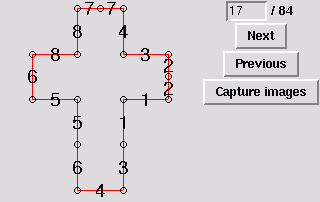
18. Hexahedron, three degree-4 vertices and two degree-3 vertices
19. Tetrahedron
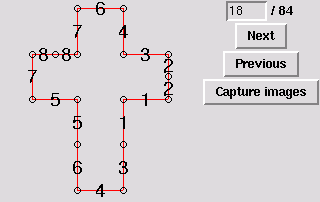
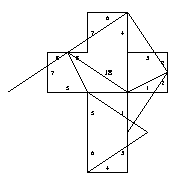
20. Pyramid with quadrangular base
21. Mirror polytope of 2
22. Same polytope as 20
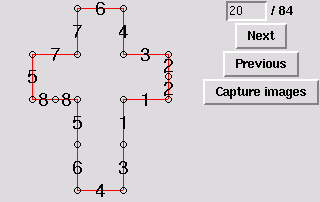
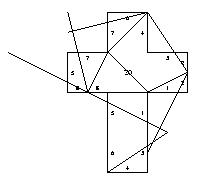
23. Gluing symmetric to 7
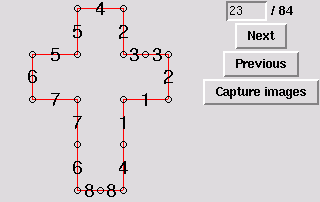
24. Hexahedron, three degree-4 vertices and two degree-3 vertices
25. Mirror polytope of 20
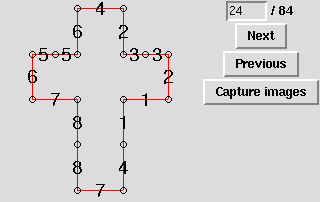
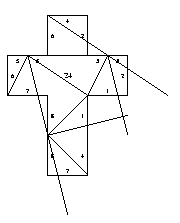
26. Gluing symmetric to 18
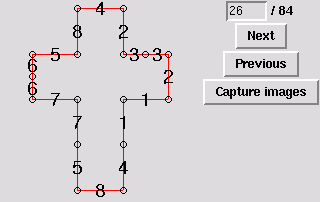
27. Gluing symmetric to 15 [edge-to-edge]
28. Same polytope as 11
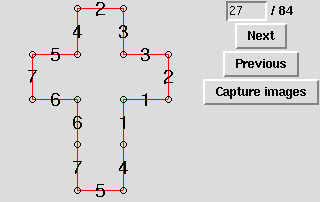
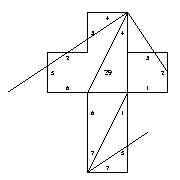
29. Same polytope as 34 [edge-to-edge]
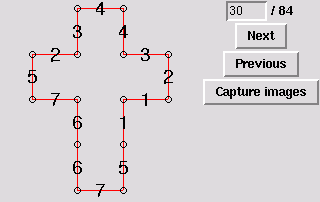
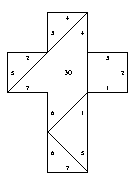
30. Doubly covered quadrangle [edge-to-edge]
31. Octahedron, two degree-5 vertices, two degree-4 vertices, and two degree-3 vertices
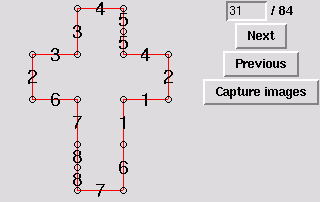
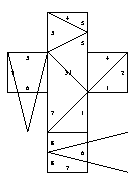
32. Octahedron, two degree-5 vertices, two degree-4 vertices, and two degree-3 vertices
33. Mirror polytope of 32
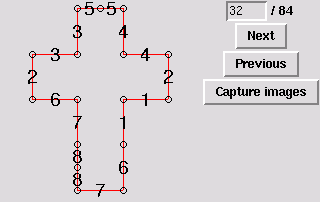
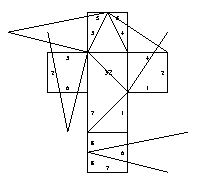
34. Tetrahedron [edge-to-edge]
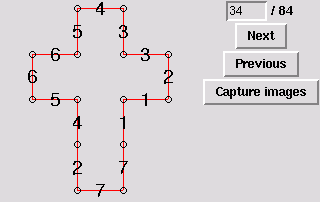
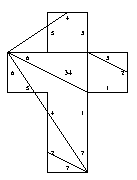
35. Gluing symmetric to 29 [edge-to-edge]
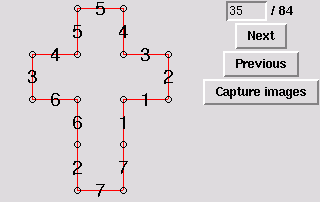
36. Gluing symmetric to 10
37. Gluing symmetric to 4
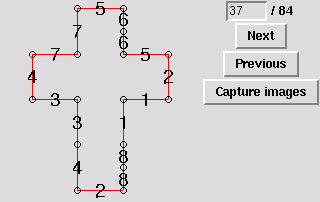
38. Gluing symmetric to 21
39. Same polytope as 3
40. Gluing symmetric to 8
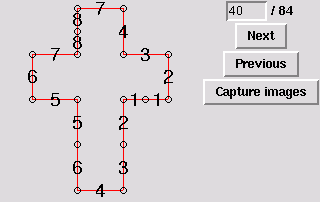
41. Gluing symmetric to 2
42. Gluing symmetric to 25
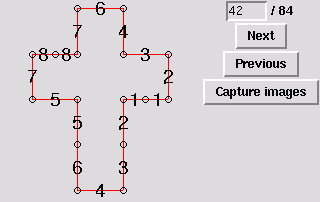
43. Reflectionally symmetric tetrahedron
44. Same polytope as 24
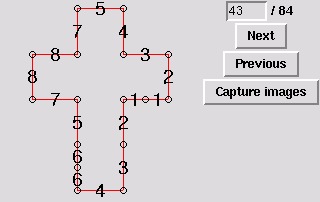
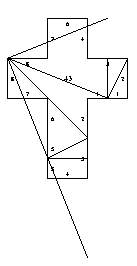
45. Gluing symmetric to 39
46. Same polytope as 18
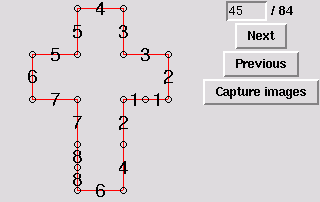
47. Gluing symmetric to 6
48. Same polytope as 20
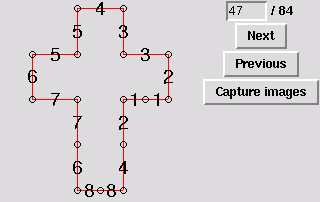
49. Gluing symmetric to 44
50. Gluing symmetric to 20
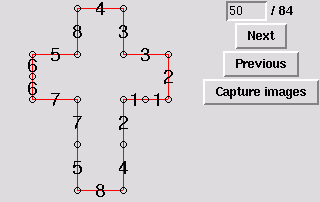
51. Gluing symmetric to 14
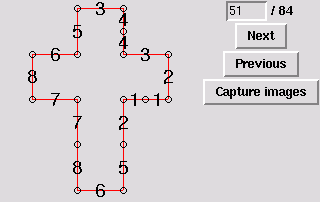
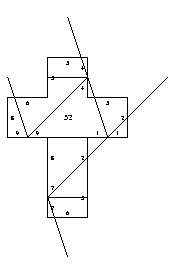
52. Tetrahedron ("almost tetrapack")
53. Tetrahedron
54. Mirror polytope of 19
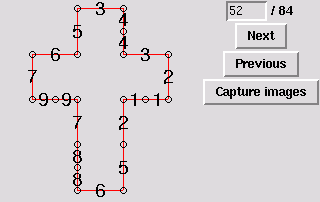
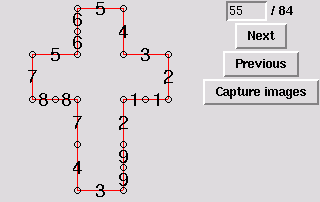
55. Gluing symmetric to 52
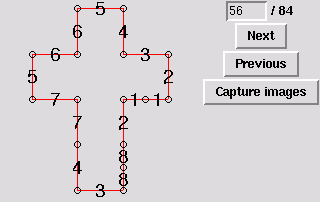
56. Gluing symmetric to 28
57. Gluing symmetric to 13 [edge-to-edge]
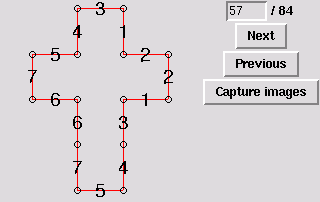
58. Gluing symmetric to 54
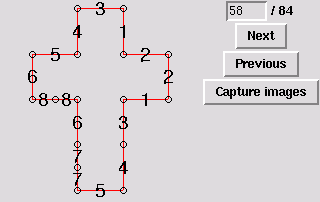
59. Gluing symmetric to 34 [edge-to-edge]
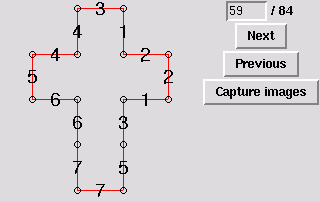
60. Same polytope as 30 [edge-to-edge]
61. Doubly covered quadrangle
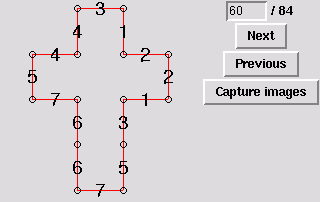
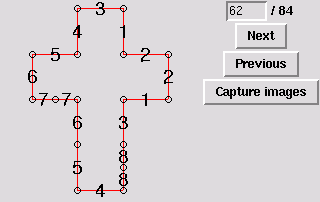
62. Gluing symmetric to 43
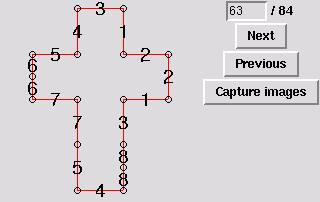
63. Gluing symmetric to 19
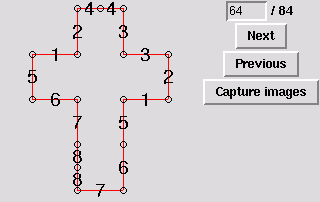
64. Octahedron, two degree-5 vertices, two degree-4 vertices,
and two degree-2 vertices
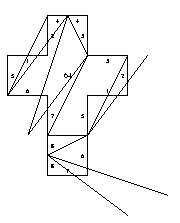
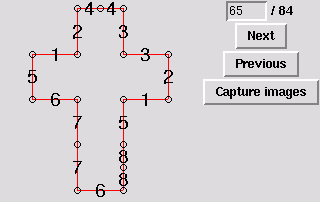
65. Hexahedron, three degree-4 vertices and two degree-3 vertices
66. Same polytope as 65
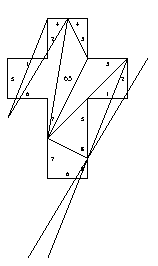
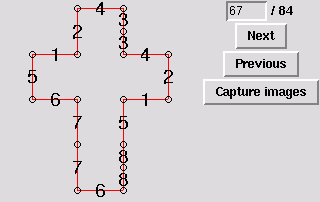
67. Rotationally symmetric tetrahedron
68. Gluing symmetric to 64
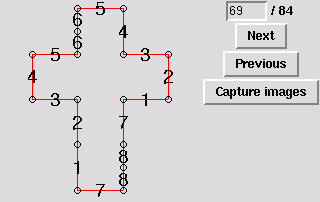
69. Gluing symmetric to 66
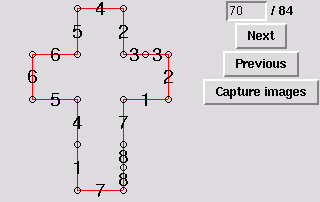
70. Gluing symmetric to 61
71. Gluing symmetric to 53
72. Gluing symmetric to 33
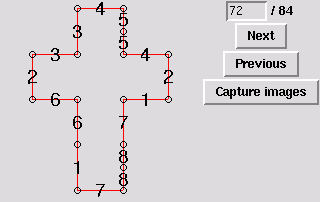
73. Gluing symmetric to 32
74. Gluing symmetric to 31
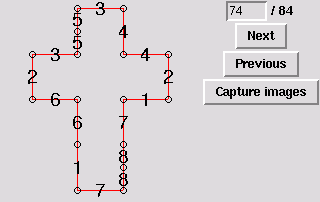
75. Gluing symmetric to 12 [edge-to-edge]
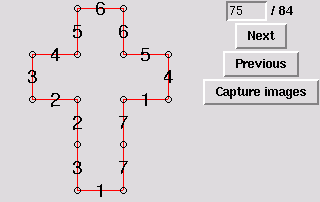
76. Gluing symmetric to 11
77. Gluing symmetric to 5 [edge-to-edge]
78. Gluing symmetric to 30 [edge-to-edge]
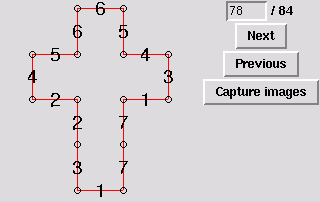
79. Gluing symmetric to 24
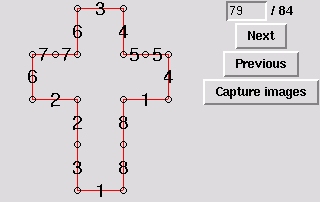
80. Gluing symmetric to 22
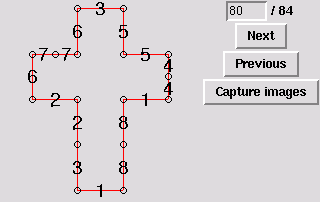
81. Gluing symmetric to 65
82. Gluing symmetric to 67
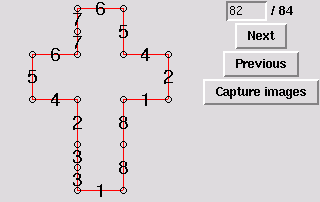
83. Gluing symmetric to 60 [edge-to-edge]
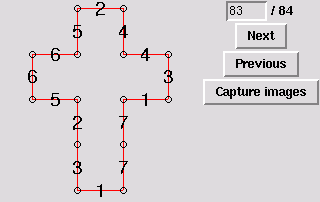
84. Gluing symmetric to 48
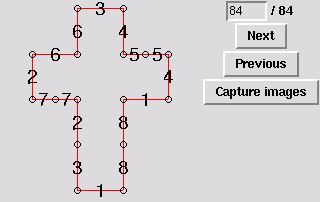
85. Gluing symmetric to 46
