Erik Demaine's Folding and Unfolding:

The Fold-and-Cut Problem

Problem

What shapes can result from the following fold-and-cut process?

Take a piece of paper.
Fold it flat.
Make one complete straight cut.
Unfold the pieces.

Are all shapes possible? Refering back to the original sheet of paper, what patterns of cuts can be achieved by this process?

The answer turns out to be any pattern of straight cuts. Try it out yourself by printing one of our several examples.

History

Wakoku Chiyekurabe by Kan Chu Sen, 1721.

The first published reference to folding and cutting of which we are aware is a Japanese book, Wakoku Chiyekurabe (Mathematical Contests), by Kan Chu Sen, published in 1721. This book contains a variety of problems for testing mathematical intelligence. One of the problems asks to fold a rectangular piece of paper flat and make one complete straight cut, so as to make a typical Japanese crest called sangaibisi, which translates to “three folded rhombics”. The author gives a solution consisting of a sequence of simple folds, each of which folds along a line. Scanned images of the relevant pages in the book are available.

Another early reference to folding and cutting is a July 1873 article “National Standards and Emblems” in Harper's New Monthly Magazine, volume 47, number 278. This article tells the story about Betsy Ross and her relation to the American flag. It claims that in 1777, George Washington and a committee of the Congress showed Betsy Ross plans for a flag with thirteen six-pointed stars, and asked whether she could make such a flag. She said that she would be willing to try, but suggested that the stars should have five points. To support her argument, she showed how easily such a star could be made, by folding a sheet of paper and making one cut with scissors. The committee decided to accept her changes, and George Washington made a new drawing, which Betsy Ross followed to make the first American flag. One method for folding and cutting a five-pointed star is described on ushistory.org's Betsy Ross page. The truth of this story is unclear, but it still makes for an early reference.

Fold and cut was the basis for several early magic tricks. The earliest such reference we know is 1833, in a book called “The Girl's Own Book” by Lydia Marie Child. See The Public Paperfolding History Project for images from this and many more references.

In particular, before Houdini was a famous escape artist, he was a general magician. His 1922 book Paper Magic (E. P. Dutton & Company, pages 176–177) describes a method for making a five-pointed star. According to David Lister, this book appears to have been ghostwritten by another magician, Walter Gibson, but Houdini still may have performed the trick.

Another magician, Gerald Loe, studied the fold-and-cut idea in some detail. His 1955 book Paper Capers (Magic, Inc., Chicago) describes how to cut out arrangements of various geometric objects, such as a circular chain of stars.

Martin Gardner wrote about the fold-and-cut problem in his famous series in Scientific American (“Paper cutting”, chapter 5 of New Mathematical Diversions (Revised Edition), Mathematical Association of America, Washington, D.C., 1995.). Gardner was particularly impressed with Loe's ability to cut out any desired letter of the alphabet. He was also the first to state cutting out complex polygons as an open problem. What are the limits of this fold-and-cut process? What polygonal shapes can be cut out?

Theorem

The theorem is that every pattern (plane graph) of straight-line cuts can be made by folding and one complete straight cut. Thus it is possible to make single polygons (possibly nonconvex), multiple disjoint polygons, nested polygons, adjoining polygons, and even floating line segments and points.

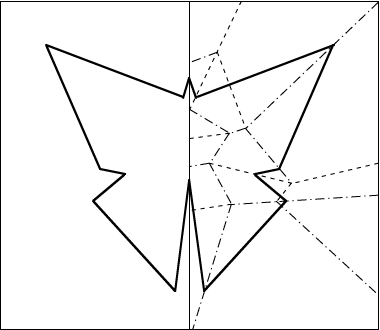
There are two methods for solving this problem, by different sets of people. I call them the straight-skeleton and disk-packing methods. You can read descriptions of them below, or watch the free online video lecture describing them:

6.849 Lecture 7

Straight-Skeleton Method

Analyzing the straight-skeleton method, from the book.

Martin Demaine, Anna Lubiw, and I solved the fold-and-cut problem using the “straight skeleton”. This structure is defined (roughly) as follows. For each face of the desired cut pattern (region between cuts), shrink the face so that the edges stay parallel and move a constant speed in a perpendicular direction. Stop whenever the boundary becomes nonsimple (intersects itself), and continue shrinking each piece. The straight skeleton is the trajectories of the vertices of the desired cut pattern during this shrinking process. Not described here are the details for vertices of degree zero and one, which require special care. For more about the straight skeleton, see Jeff Erickson's straight-skeleton page or Aichholzer et al.'s original paper about the straight skeleton.

The straight skeleton consists of the majority of the creases and achieve the desired “lining up” of cuts. In addition, there are perpendicular creases. Basically, from each vertex of the straight skeleton, we shoot a ray perpendicular to each reachable cut edge, and the ray “bounces” (reflects) through any skeleton edges it meets.

The difficult part is proving that the straight-skeleton creases together with a subset of the perpendicular creases (and a few more auxiliary creases) can be folded into a flat origami. This is done by exhibiting a folded state, that is, by demonstrating how the piece of paper looks when folded. This folded state must satisfy the properties that each face is isometrically preserved and that paper does not intersect itself.

The most detailed description is the book Geometric Folding Algorithms: Linkages, Origami, Polyhedra. The full paper (which includes all proof details) is still in progress. The longest description includes many of the proofs and was published in the Proceedings of the Japan Conference on Discrete and Computational Geometry (JCDCG'98), to appear as a volume in Lecture Notes in Computer Science. A 2-page description of the method (without proofs) appears in the Proceedings of the 10th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA'99).

This work is related to Robert Lang's TreeMaker, although it was initially developed in isolation. The intersection is that they both solve the fold-and-cut problem when the faces (shapes to be cut out) are all convex. Both TreeMaker and our work extend far beyond this common base, in different directions. Essentially, TreeMaker tries to collapse a polygon to a specified folded shape but only addresses convex polygons, whereas the straight-skeleton method focuses on the unfolded shape and addresses nonconvex and disconnected polygons.

Disk-Packing Method

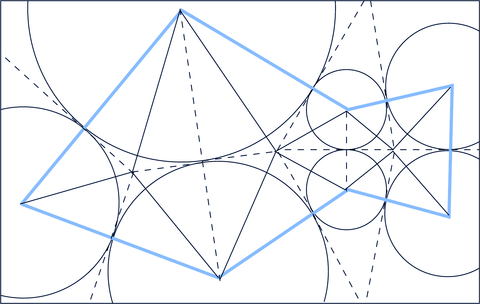
An example of the disk-packing method, from the paper.

Inspired by early versions of the straight-skeleton method, Marshall Bern, David Eppstein, Barry Hayes, and I solved the fold-and-cut problem using disk packing. Specifically, we place disks on the piece of paper, such that

the disks do not properly overlap (but may touch),
the gaps between disks have either three or four sides,
there is a disk centered at each vertex of the desired cut pattern, and
the edges of the desired cut pattern (i.e., desired cuts) are the union of radii of disks.

As a result, we can decompose the desired cut pattern by adding edges between centers of touching disks, and this results in a collection of triangles and quadrangles. We then fold each of these triangles and quadrangles using molecules that line up the boundaries of the triangles and quadrangles. This is the basic idea--a couple of tricks are needed to show that the molecules can be joined together, and a further trick is needed so that only the desired lines are the ones that come together onto a common line.

The most detailed description is the book Geometric Folding Algorithms: Linkages, Origami, Polyhedra. The paper “A Disk-Packing Algorithm for an Origami Magic Trick” also describes the method in detail, though it has some small issues. The most recent version includes some simplifications, and appears in the Proceedings of the 3rd International Meeting of Origami Science, Math, and Education (OSME 2001). The original version was published in the Proceedings of the International Conference on Fun with Algorithms (FUN'98).

Our use of disk packing is quite different from Robert Lang's TreeMaker, although it is intriguing that the same method comes up in two different contexts in origami mathematics.

Try out our new simple fold and cut font!

A 2010 paper with Martin Demaine, Andrea Hawksley, Hiro Ito, Po-Ru Loh, Shelly Manber, and Omari Stephens considers what happens when we restrict the folds to a sequence of simple folds, folding along a single line at a time.
Check out our new font based on simple fold and cut!

Ivars Peterson briefly describes the fold-and-cut results in his article, “Fold-and-Cut Magic”, which appears in Science News, volume 162, number 22, November 30, 2002.

Joseph O'Rourke briefly describes the two fold-and-cut methods in his “Computational Geometry Column 36”, which appears in International Journal of Computational Geometry and Applications, volume 9, number 6, pages 615-618, 1999; and SIGACT News, volume 30, number 3, issue 112, September 1999, pages 35-38.

One application of the fold-and-cut theorem is the design of the logo for CCCG 2001.

Some of our earlier papers on the fold-and-cut problem are the following:

The technical report “Computing Extreme Origami Bases” studies the special case of cutting out a convex polygon. In this case, we can not only compute a folded state exists, but we also provide the continuous motion of the paper through time that reaches this folded state. In fact, the motion can be achieved while keeping rigid the regions between creases rigid, called rigid origami.
“Planar Drawings of Origami Polyhedra” studies some properties of the foldings of convex polygons using graph drawing. A 2-page summary was published in the Proceedings of the 6th Symposium on Graph Drawing (GD'98). The full version is a technical report.

Last updated March 28, 2024 by Erik Demaine. — Accessibility