Pushing Blocks
Categorization
Pushing-block puzzles are a popular form of one-player game in which an agent
or robot moves around and pushes unit-square obstacles in a square grid.
There are several variations on the rules, depending on the following aspects:
- The strength of the robot: How many blocks can the robot push at once?
- Can blocks be tied to the board, making them unpushable?
- How far do blocks move when pushed?
Typically blocks move only one space at a time,
but in the more icy/frictionless model of
PushPush,
blocks slide as far as possible.
- What is the goal of the robot? There are two common targets:
- The robot should reach a particular position (the exit),
as in the various Push puzzles.
- The movable blocks should all be placed on marked
(but undistinguished) target squares, as in the Sokoban puzzle.
- Various restrictions can be placed on the solution path.
In particular, what if the robot is not allowed to revisit any square?
Complexity
Since 1991, basically all variations of pushing-block puzzles have been
explored from the point of view of computational complexity. The short summary
is that pushing blocks is at least NP-hard and at most in PSPACE, no matter
which combination of parameters you choose. The main open questions are
whether various versions are in NP or PSPACE-complete.
Surveys on these results can be found in most papers on the subject,
in particular the latest
Push-X paper and the preceding
Push-1 paper; as well as in
my survey
paper on combinatorial games and puzzles.
I also give a brief overview here.
Versions
Sokoban
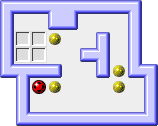
Perhaps the best-known example of a pushing-block puzzle is the computer game
Sokoban.
Here (1) the robot can push only one block at a time, (2)
blocks can be tied to the board, (3) blocks move only one space at a time, and
(4) the goal is to place the movable blocks on specified target locations (but
any block can be placed on any target).
This game was invented by Hiroyuki Imabayashi of Thinking Rabitt Co. in 1982;
see a history
of Sokoban.
There are many implementations of Sokoban and puzzles available,
most of which are freely available. For example:
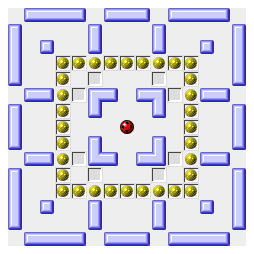
- Sokoban,
an extensive Windows implementation by Björn Källmark
with over 450 puzzles
- SokobanMac,
an excellent Macintosh implementation by Scott Lindhurst,
plus a repository for hundreds of collected puzzles.
[The three images on the right are taken from this webpage.]
- A Java implementation
by Pimpernel Online with 20 puzzles
- XSokoban,
an X-Windows implementation
- Over 350 puzzles
designed by David Skinner
- Puzzles
designed by Yoshio Murase and generated by a program of his,
including many links to pages and papers on solving Sokoban and
generating puzzles by a computer in practice
- Shockoban,
a Shockwave implementation
- The Yahoo! Sokoban
group contains discussion areas with hints and additional puzzles
- SokoMind, a Windows implementation
by Gerald Holler
that includes a variation (SokoMind Plus) in which each blocks must move
to a specific target location,
and a repository of over a thousand puzzles the standard version
and this variation
- Soko,
a Windows implementation by Mark McIntyre
that includes a level editor and several new puzzles
 NP-hardness of Sokoban was established by Dorit Dor and Uri Zwick in their 1995
paper “SOKOBAN
and other
motion planning problems”, appearing in Computational Geometry: Theory
and Applications, volume 13, number 4, 1999, pages 215--228.
PSPACE-completeness was established by Joseph Culberson in his 1997 paper
“Sokoban
is PSPACE-complete”, appearing in Proceedings of the International
Conference on Fun with Algorithms, June 1998, pages 65-76.
NP-hardness of Sokoban was established by Dorit Dor and Uri Zwick in their 1995
paper “SOKOBAN
and other
motion planning problems”, appearing in Computational Geometry: Theory
and Applications, volume 13, number 4, 1999, pages 215--228.
PSPACE-completeness was established by Joseph Culberson in his 1997 paper
“Sokoban
is PSPACE-complete”, appearing in Proceedings of the International
Conference on Fun with Algorithms, June 1998, pages 65-76.
Origins
The formal study of robot-manipulation puzzles was initiated by Gordon Wilfong
in 1991. He proved NP-hardness of a variation not captured by the
categorization above, in which L-shaped pieces can be both pushed and pulled by
the robot.
Push[Push]-1/k/*-[X]
The formal study of square-block-pushing puzzles was initiated by Arundhati
Dhagat and Joseph O'Rourke in 1992. They proved NP-hardness of a version that
has since been dubbed Push-* with fixed blocks. In general, there are
many variations under the "Push" umbrella:
- In Push...-1, the robot can push only one block at once, and
more generally in Push...-k the robot can push at most
k blocks at once, whereas in Push...-*, the robot has the
strength to push any number of blocks.
- There are two versions of every puzzle, in which either blocks can be
tied to the board (with fixed blocks) or not
(without fixed blocks). This issue is particularly relevant
in Push...-*, although it may make a difference even in Push-k
where a (k+1)-by-(k+1) square of blocks is
effectively immobile.
- In Push-... blocks move only one square at a time, whereas in
PushPush-... blocks slide to their maximal extent.
- The goal of the robot is to reach a particular target location.
- In the Push...-X variation, the solution path is not allowed to
cross itself.
Thus, the 16(+) puzzles are Push-k, Push-*, PushPush-k,
PushPush-*, Push-k-X, Push-*-X, PushPush-k-X, PushPush-*-X, all
with or without fixed blcoks.
While there are various papers proving NP-hardness of specific versions
(see the surveys cited above and in particular the webpages cited below),
the NP-hardness of all of these puzzles can be established by just the latest
two papers:
I have seperate webpages on two flavors of Push puzzles, which describe joint
work with Martin Demaine and Joseph O'Rourke:
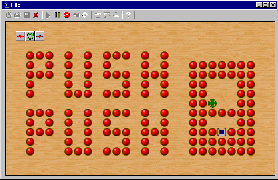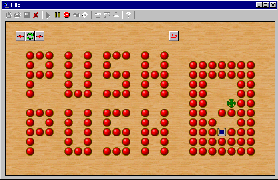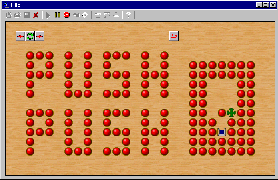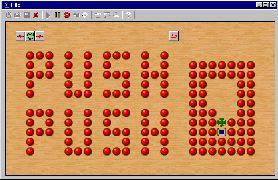
- PushPush-1:
Blocks slide as far as possible, and only one block can be pushed at
a time. Includes my computer implementation of this game,
and links to related implementations.
- Push-1:
Blocks slide one square at a time, and only one block can be pushed
at a time.



 NP-hardness of Sokoban was established by Dorit Dor and Uri Zwick in their 1995
paper “SOKOBAN
and other
motion planning problems”, appearing in Computational Geometry: Theory
and Applications, volume 13, number 4, 1999, pages 215--228.
PSPACE-completeness was established by Joseph Culberson in his 1997 paper
“Sokoban
is PSPACE-complete”, appearing in Proceedings of the International
Conference on Fun with Algorithms, June 1998, pages 65-76.
NP-hardness of Sokoban was established by Dorit Dor and Uri Zwick in their 1995
paper “SOKOBAN
and other
motion planning problems”, appearing in Computational Geometry: Theory
and Applications, volume 13, number 4, 1999, pages 215--228.
PSPACE-completeness was established by Joseph Culberson in his 1997 paper
“Sokoban
is PSPACE-complete”, appearing in Proceedings of the International
Conference on Fun with Algorithms, June 1998, pages 65-76.
